
中学生・高校生にもなると、皆おしゃれを楽しむようになるものです。
以前、高校生の女の子が「今日何が違うかわかる??」と目をキラキラさせて聞いてきたのですが、
「前髪切った?」
「メガネ変えた?」
「ピアス新しいやつだ!」
とことごとく外した結果、「もう知らない!!!」とぷんぷんで他のところに行ってしまいました。
答えは「初めてお化粧してみた」でした。くそぅ…笑
どうも、時々全くおしゃれに気が付かない鈍感なひつじぃです。
はじめに
今回から、「算数障害」についての基礎知識を綴っていこうと思います。
目的は二つです。
●社会的に認知が乏しい「算数障害」を知ってほしい
●「自分は『算数障害』かも?」と気づき、適した学習方法を見つけて、ラクに学習をしてほしい
残念ながら、未だ算数障害は社会的な認知が乏しい状況にあります。
この記事では、そもそも算数障害とは何か?その歴史から細かな特徴まで、基礎的な部分を書いていきます。

算数障害グレーゾーンだけど気づいてない人、沢山いると思う!
算数障害(ディスカリキュア)とは何か?
算数障害とは
算数障害は、学習障害(LD)の種類の一つとされます。
簡単に説明すると、対人コミュニケーションなどには問題がなく、国語や社会などの科目も周囲と変わらない習熟を見せているのに算数だけが極端に苦手な状態です。
算数障害の発症率は5~7%(20人に1人!!)と言われており、これは読字障害・書字障害と同程度の割合となっています。
学習障害には、6つの領域が存在します。
「聞く」「話す」「読む」「書く」「計算する」「推論する」です。
算数障害は、このうち「計算する」と「推論する」に困難があるとされます。
読字障害やADHDとの合併が知られており、特に読字障害は算数障害のある子どものうち40~60%を占めるという報告もあります。
主な困りごと
算数障害の方の主な困りごととして、以下があげられます。
・モノを数えることが難しい
・数の大きい、小さいが分からない
・計算することが難しい
・およその量が分からない
・文章題の出来事がイメージできない
・足し算、引き算、掛け算、割り算…どの計算を使って解けばよいか分からない
これらの困りごとに対し、「どうしてこのような状態になるのか」はこの記事の後半に、「どう対処したらよいのか」は、後日の記事にて説明をしていきます。
診断
DSM-5では、限局性学習症・限局性学習障害として、書字障害・読字障害を含め、ひとくくりで説明がされています。
A.学習や学業的技能の使用に困難があり、その困難を対象とした介入が提供されているにも関わらず、以下の症状の少なくとも1つが存在し、少なくとも6ヶ月間持続していることで明らかになる:
- 不適格または速度が遅く、努力を要する読字(例:単語を間違ってまたはゆっくりとためらいがちに音読する、しばしば言葉をあてずっぽうに言う、言葉を発音することの困難さを持つ)
- 読んでいるものの意味を理解することの困難さ(例:文章を正確に読む場合があるが、読んでいるものの繋がり、関係、意味するもの、またはより深い意味を理解していないかもしれない)
- 綴字の困難さ(例:母音や子音を付け加えたり、入れ忘れたり、置き換えたりするかもしれない)
- 書字表出の困難さ(例:文章の中で複数の文法または句読点の間違いをする、段落のまとめ方が下手、思考の書字表出に明確さがない)
- 数字の概念、数値、または計算を習得することの困難さ(例:数字、その大小、及び関係の理解に乏しい、1桁の足し算を行うのに同級生がやるように数学的事実を思い浮かべるのではなく指を折って数える、算術計算の途中で迷ってしまい方法を変更するかもしれない)
- 数学的推論の困難さ(例:定量的問題を溶くために、数学的概念、数学的事実、または数学的方法を適用することが非常に困難である)
B.欠陥のある学業的技能は、その人の暦年齢に期待されるよりも著名にかつ定量的に低く、学業または職業遂行能力、または、日常生活活動に意味のある障害を引き起こしており、個別施行の標準化された到達尺度および総合的な臨床評価で確認されている。17歳以上の人においては、確認された学習困難の経歴は標準化された評価の代わりにして良いかもしれない
C.学習困難は学齢期に始まるが、欠陥のある学業的技能に対する要求が、その人の限られた能力を超えるまでは完全には明らかにはならないかもしれない(例:時間制限のある試験、厳しい締切期限内に長く複雑な報告書を読んだり書いたりすること、過度に重い学業的負荷)
D.学習困難は知的能力障害群、非矯正視力または聴力、他の精神または神経疾患、心理社会的逆境、学業的指導に用いる言語の習熟度不足、または不適切な教育的指導によってはうまく説明されない
この基準に照らして学習障害と診断され、かつ以下の傾向が強いと判断されると算数障害(ディスカリキュア)と言えます。
算数の障害を伴う:
・数の感覚
・数学的事実の記憶
・計算の正確さまたは流暢性
・数学的数理の正確さ
また、ICD-10では、以下のように述べられています。
ただ単に一般的な知的障害あるいは非常に不適切な学校教育だけでは説明できないような算数能力の特異的障害である。この障害は、代数学、三角法、幾何学または微積分学のようなより抽象的な数学的能力よりは、むしろ加減乗除のような基本的な計算能力の習得に現れる。
残念ながら、現在「算数障害」と診断できる医療機関はありません。
今現在、日本では標準化された診断基準が存在せず、医学の診断基準では算数障害という診断名は使われません。診断名としては前述のアメリカ精神医学会のDSM-5以降におけるSLD(限局性学習症)になります。
そもそも診断というものが、「ヘルプを求めるためのモノ」という側面を大きく持っているため、社会的に認知が乏しく十分な支援を受けることが難しい現在では、算数障害の診断に大きな価値を持たせられないのも事実です。
今後社会的な認知が広がり、診断もより手軽に効果的に受けられるようになることを願い、記事を書きます。
検査
「計算する」「推論する」の領域は、WISC・WAIS、KABC-Ⅱといった検査にも含まれており、対応しています。
診断と同じく算数障害単体の具体的な指標はなく、学習障害の基準で総合的に判断されます。
学習障害に関しては後日別記事にて。
参考までに、日本心理学会「心理学ワールド」70号P.20に記載されたチェックリストを引用します。
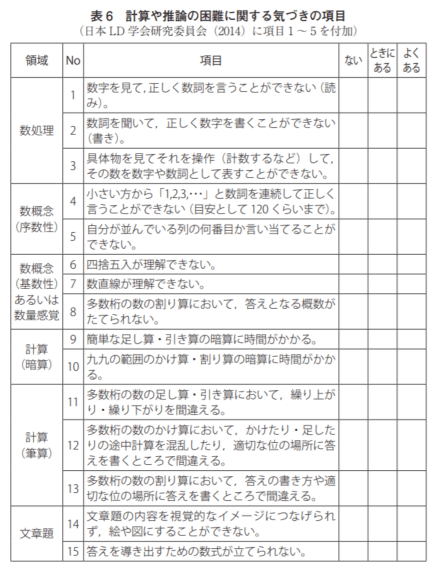
表6のようなチェックリストに多く当てはまる問題を抱える子どもたちには,必ず個別の知能検査を行うなどして,全体的な知的能力水準がどれくらいか,また,知的能力を構成する下位の認知能力の強い・弱い能力を同定しておくことが重要である。全体的な知的能力水準が下である場合には,その子どもの抽象化能力に限界はあるが,偏りがある場合には,指導によっては理解できることも多いはずである。
日本心理学会「心理学ワールド」70号P.20
歴史
子どもの算数の問題は、Strauss & Wernerにより1938年の子どもの脳損傷の研究から取り上げられている。
知的能力は低くないのに、先天的に算数の困難があるという子どもの計算障害については、1960年代頃に研究が始まっている。
Kosc(1974)やBadian(1983)により、算数障害の分類が行われたが、これらの分類は機能的ではなかった。
Temple(1989, 1991)は、子どもの算数障害も基本的には成人で考えてきたMcCloskeyらのモデルに当てはめて考えられると述べた。
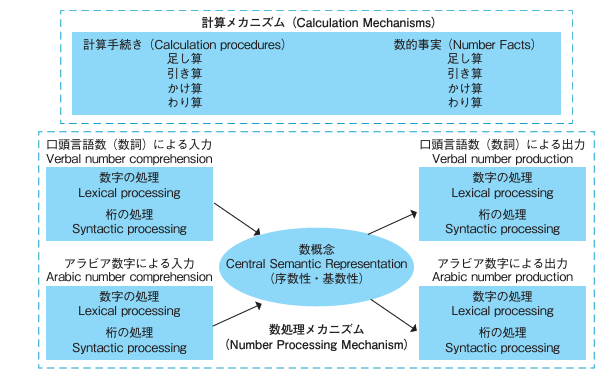
McCloskeyらによる「算数に関する認知モデル」
日本心理学会「心理学ワールド」70号P.18
一方Kirkは、1962年にアメリカで学習障害という用語を提唱した。欧米ではかなりの程度の子どもたちに読み書き障害があることが知られており、そのことを学習障害とまとめたのであるが、その中にはすでに算数の困難も含まれていた。
その後1975年、全障害児教育法において学習障害は初めて支援される対象となったが、この定義の中でも算数の困難が取り上げられている。
算数障害の領域
領域の分類
DSM-5では、算数障害の領域を、以下のように考えます。
算数に障害のある特異的学習障害(Specific Learning Disorder with impairment in mathematics)
①数感覚(Number sense):数量概念
②数的事実の記憶(Memorization of arithmetic fact):暗算
③正確で流暢な計算(accurate or fluent calculation):筆算
④正確な数学的推論(accurate math reasoning):文章題
これに、子どもの場合には「数という概念を獲得していく過程である」ことを考慮、また前述のMcCloskeyらによる「算数に関する認知モデル」の「数処理」を加え整理したものが、以下となります。
①数処理:数の大小比較や操作・数の読み書き
②数概念:序数性と基数性
③計算:四則演算の暗算(数的事実),筆算(手続き)
④推論:文章題を解く
熊谷(2013) より
今後の記事では、上記の表の分類を使用していきます。
上記の表と、DSM-5を比べると、下記の表のように対応します。
上記の表
①数処理
②数概念
③計算
④推論
DSM-5
⇒ 明示なし
⇒ ①数感覚
⇒ ②数的事実の記憶、③正確で流暢な計算
⇒ ④正確な数的推論
数処理
数詞、数字、具体物の対応関係を理解すること。
数詞…聴覚的シンボル。下の例の場合、「イチ」という音。
数字…視覚的シンボル。下の例の場合、「1」という文字。
具体物…視覚的で動かせるもの。下の例の場合、リンゴ1つ。
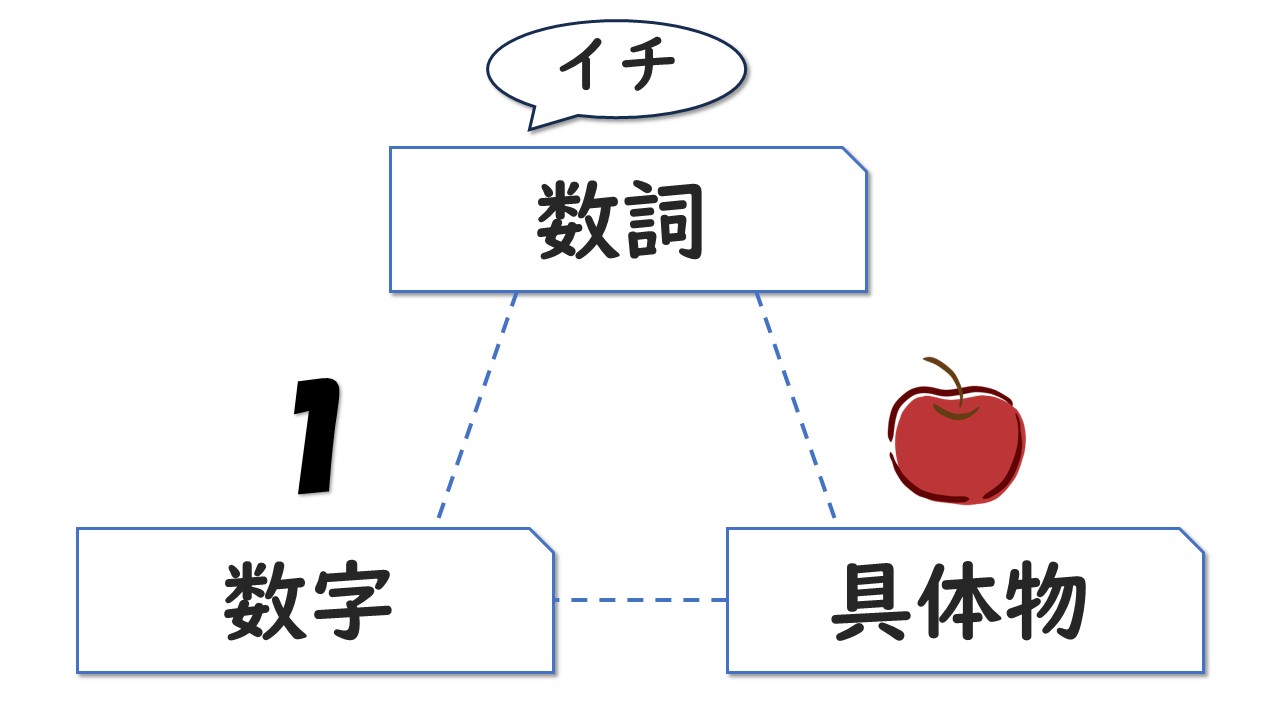
数処理の理解に困難がある場合、例えば「リンゴが1つだけある」という具体物の状況は把握できても、それが数字の「1」と数詞の「イチ」に結びつかず、「1つある」ということを表現できない、ということになる。
この数処理の難しいところは、数詞は聴覚、数字は視覚、具体物は視覚や触覚と、それぞれ習得するために使用する感覚が違うこと。
例えば聴覚に困難がある場合、数詞の習得が難しくなる。
また、それらの感覚を1つの概念に統合(上の例では「1」)する段階では、脳処理がどこで追いついていないのか把握する必要がある。
数処理の段階は、他のすべてのものに先だって形成されなければならないため、困難がある場合は早期に発見されると思われる。
数概念
数の性質を理解すること。
数には順番を表す序数性、量を表す基数性という2つの側面があることを理解する。
能力にアンバランスなところがある人は、どちらかがうまく習得できない場合がある。
これらは数処理の次の段階にあるものである。
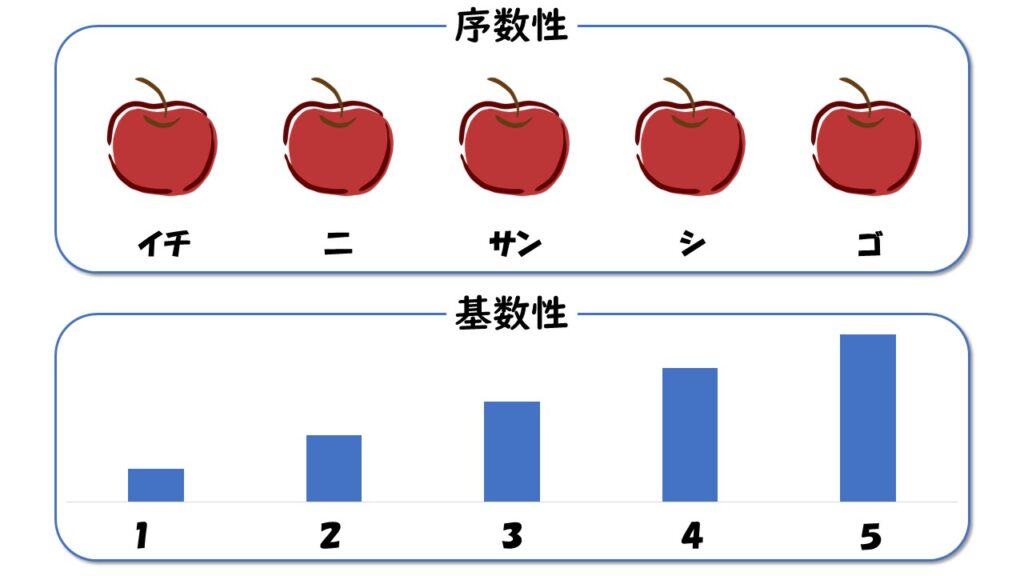
リンゴなどの「分離量」(数えることができる量)、水などの「連続量」(数えることができない量)の理解は、数概念とはまた別とされる。
数概念の理解に困難がある場合、「リンゴが1つ」「リンゴが2つ」と順に数えていくことが難しくなると考えられる。
順に数えていく、ということは足し算・引き算を具体物の面から習得するのに不可欠であり、数字上でなく日常での計算自体に困難を抱えることになる。
計算
計算をすること。
この領域は、暗算と筆算に分けて考える。
この場合の「暗算」とは「加減算で和が20までの計算、乗除算で九九までの範囲の計算」、「筆算」とは「それ以上の数の計算」とされる。
暗算ができるようになるためには、5や10の合成分解ができなければならない。
そのなかで、具体物(リンゴなど)から半具体物(おはじきなど数えるための道具)、半具体物から数、という過程をたどって「数」を理解しているかを把握する必要がある。
筆算には、くり上がりくり下がりの手続きの問題と、桁が二つ以上の数字の空間的な配置(筆算をする際にどこになんの数字が書かれるか)とその意味が理解できている必要がある。
計算の理解に困難がある場合、文字そのまま計算が難しい、ということになる。
具体物→半具体物→数といった過程がうまく辿れていないと「手で数える」段階を抜けられないし、筆算の空間的な配置が理解できていないと途中式を書いている際にどんどん桁がずれていってしまう。
ひつじぃとハリーが運営している無料学習プリントサイト「といろプリント」では、算数障害に配慮した学習プリントを更新しています。
各単元の学習を、認知処理優位・認知特性に合わせてプリントの形を選び、同じ内容を違う方法で学ぶことができる学習プリントサイトです。
ひとつひとつ丁寧に作っているため少しずつの更新になりますが、ゆくゆくは幼児・小学校・中学校の算数国語を全て網羅し、その他の教科やプリント教材にも力を入れていこうと考えています。
計算の合成分解、くり上がりの概念に関する学習プリントのリンクを、下に貼っておきます。
無料なので是非、ご活用ください。





数的推論(文章題)
数を扱う文章から、計算式を立式して問題を解くこと。
数的推論では、統合過程(言葉から視覚的なイメージへの変換)と、プランニング過程(立式をする)という2つの過程が非常に大事になる。
前提として、読み書き障害ではないこと、読み書きに困難がないことを確認する必要がある。
数的推論の理解に困難がある場合、文章題になると途端に解けないという状況が発生する。
この困難を、「2つの過程に分けて、どこでつまずいているか・困難があるかを把握する」ということが何より大切だと感じる。
おわりに
今回は、算数障害の基礎知識として、算数障害の定義からその領域までを見ていきました。
数的推論などは「あれ?これあてはまるんじゃ…」と思う方、かなりいるんじゃないでしょうか?
私も現場で見ていて、定型発達・非定型発達(発達障害)問わず、色々なところで「あ~この子、半具体物で止まってるな」「プランニング過程が苦手なんだなぁ」とか感じることが山ほどありました。
「算数障害」として捉えなくても、「算数の苦手」を考える上でこれらの知識はとても役に立ちます。
それでは次回から、それぞれの領域に関してどのようにアプローチをしていったら良いのか、具体的にご紹介していきます。
みんなで打倒!算数苦手問題!





コメント