
近年の研究で、日本のみかんには「ミカニウム」という独自の栄養素が含まれており、
精神を健康に保ち、免疫力をあげる効果があるそうです。
嘘です。私がみかん食べたいだけです。
ひつじぃです。
はじめに
今回は、算数障害の困りごとに対し、どのように考え対処すべきか・支援すべきかの前提知識を書いていきます。
繰り返しますが、定型発達の人の「算数が苦手」にも大いに使える内容です。
少し変わった視点から見る「算数が得意になる方法」だと思って、読んでください。
それでは、いってみよ~。

算数ってほんと難しい…。みんな苦手なところが違ったりするよね。
四領域の考え方
前回の記事で、算数障害の四領域のお話をしました。
これら四つの四領域がどのように算数の学習と対応するのか、整理をしていきます。
四領域の構成
まず下の図を見てください。
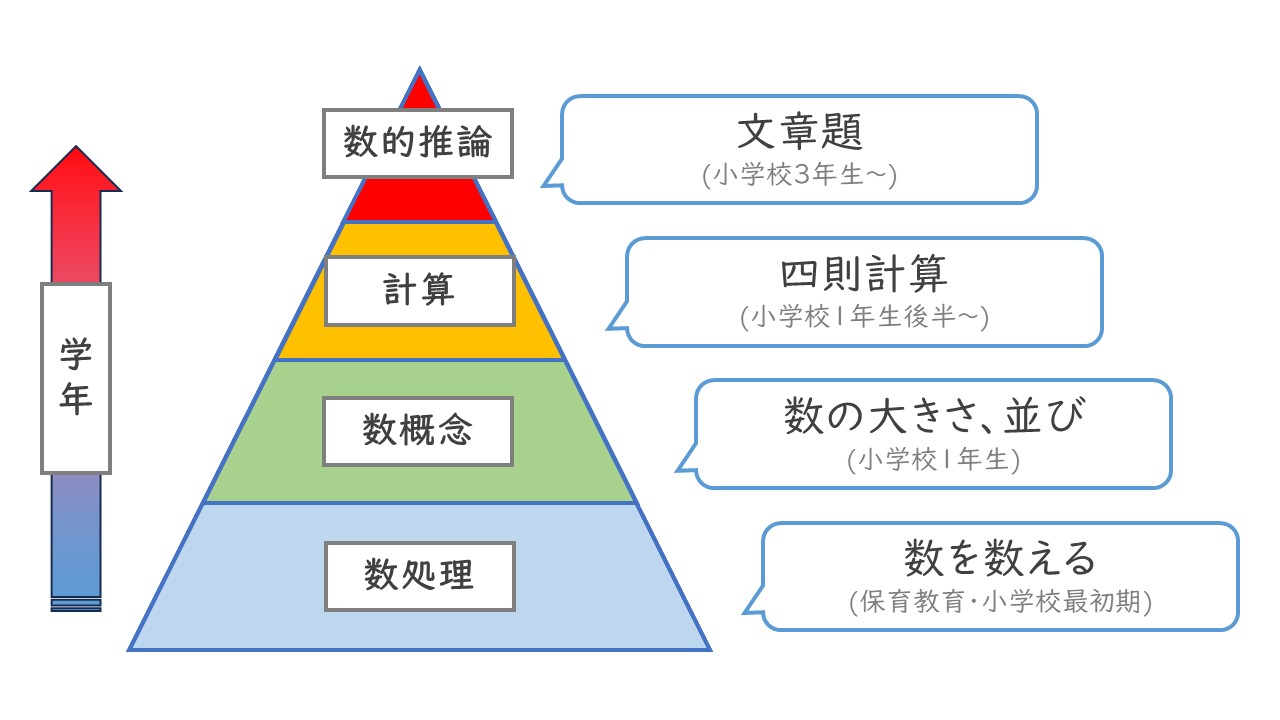
上記の図は、四領域の構成を表しています。
まず初めに「数詞・数字・具体物の関係」である「数処理」が習得され、
これらが理解できた次に「序数性・基数性」という「数概念」が習得できる。
そしてこれら「数の理解」があって初めて「数と数の操作」という「計算」が習得される。
計算ができて初めて「様々な数の変化や操作の推論」という「数的推論」が習得できる。
この順番は変わらないものであって、どの過程で困難が発生しているか把握することが、支援の第一歩となります。
四領域の関係性
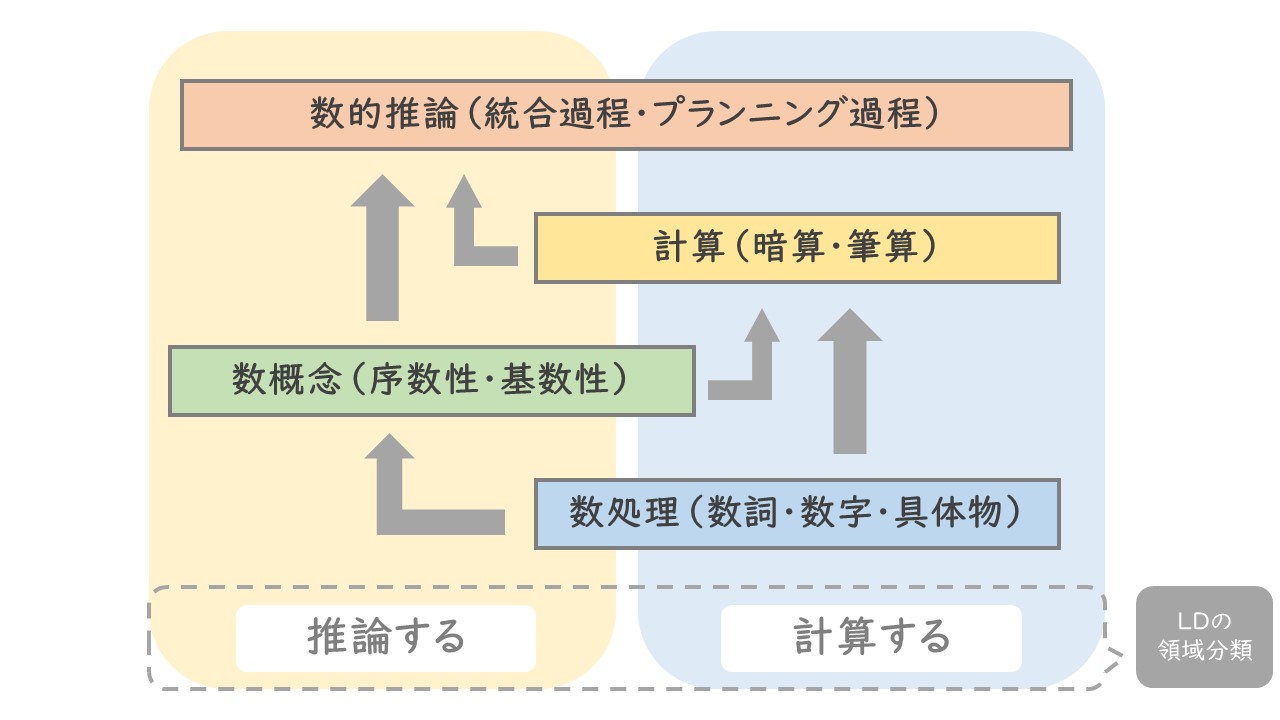
前項で「四領域には習得順がある」としましたが、必ずしも順に進んでいかないと習得できない、というわけではありません。
数処理は計算の前段階であり、数概念は数的推論の数の変化を考える前段階となります。
方法をそのまま覚える、という継次処理的な能力にのみ注目するならば、数処理が習得できていれば計算が習得できます(解き方の丸暗記で筆算を計算する等)。
数の仕組みから理解する、という同時処理的な能力にのみ注目するならば、数概念が習得できていれば数的推論が習得できます(計算ができなくても図や表使って文章題を解ける等)。
同時処理・継次処理といった認知処理能力は、算数障害を考える上でとても大事な要素となります。
この内容は後に説明をします。
また、LDの六領域に照らし合わせると、数処理・計算が「計算する」、数概念が「推論する」、数的推論がその両方に当てはまります。
学習内容との対応
こちらは、東書の学習系統表です。
tousyo-math中高含めたものは、こちらから見れます。
https://ten.tokyo-shoseki.co.jp/text/hs/sugaku/data/sugaku_16661_dm08.pdf
これを見ると、一年生は数概念と計算をメインに、二年生から計算が本格化し、三年生から数的推論が本格化することが分かります。
数処理も一年生の一番始めに触れるはずですが、学習内容としては明示されていません。ということは、数処理は保育教育で習得しているよね、ということが前提になっているのです。
ここで、保育教育での数処理の習得が難しかった場合、ただでさえ大きく環境が変わり緊張の中にいる小学校一年生の、最初の数概念の授業から「分からない」という状況になります。
また、数概念であれば一年生前半、計算であれば一年生後半から困難が見え始め、数的推論であれば三年生から「応用問題」として入ってくる文章題がとても難しくなることでしょう。
要するに「小学校三年生までに算数障害の大体の困難は困りごととして見えてくる」ということです。
裏を返すと「小学校三年生までに困難を見つけ、適切に対処をすることが望ましい」ということです。
同時処理能力と継次処理能力
前述した「同時処理・継次処理といった認知処理能力は、算数障害を考える上でもとても大事な要素となる」に触れていきます。
認知処理特性については、こちらの記事に詳しく書いてあります。


算数の内容でも、継次処理・同時処理の両方の能力を使って習得していくことになりますが、各単元で主に使うことになる認知処理能力には、偏りがあります。
また、同じ内容でも得意な認知処理能力を使って習得することができる面もあります。
例えば数処理ですが、「1~9」を数える能力は、系列的に覚え理解する「継次処理能力」が主に関わります。
「10~」の数は、桁の構造を理解して数字を構成する「同時処理能力」が主に関わります。
こういった面から、同じ数処理の中でも、部分によって得意・苦手が分かれることがあり、その場合は認知処理能力の偏りを意識して学習の補助を進めていくことができます。
例えば「1~9」を数える能力では、「1からどれくらい離れた数か」と視覚的に数直線に表して理解することで、同時処理的に考えることが可能です。
「10~」の数は、「10」「20」「30」…といったまとまりの表を作り、「10から数える」という形で系列的に数えることで、継次処理的に考えることが可能です。
複雑な文章題を「継次処理優位だから、解き方の丸暗記で解く!」というのは限界があるように、確かに工夫にも限度はあるのですが、小学校・中学校レベルの内容であれば認知処理特性に合わせて学習の習得方法を変えることは十分に可能です。
具体的な方法については、今後の「算数障害の具体的な支援法②~」と、「認知処理特性③~」にまとめていきますので、よろしければご覧ください。
また、といろプリントを使っていただければ、自分に合った認知処理能力で取り組めます。
プリントして解くだけなので、こちらの方がすぐに実践できておすすめです。
おわりに
今回は、算数障害へアプローチするための前提知識について見ていきました。
正直この三・四倍くらいの知識は必要になると思うのですが、それは次回以降の記事にて少しずつ説明していきますね。
算数障害も読字・書字障害と同じく「苦手」から「全くできない」まで、その程度は様々です。
しかし、「苦手」だからまだラク、「全くできない」から大変、というわけではありません。
「苦手」なら「しんどさに気づいてもらえない」「苦手ならできるはず」と、違った困り感が出てくるのです。
程度が軽いことと、困り感が小さいことは、全くイコールではありません。これは他の障害深度に関しても同じです。
苦手だってしんどいんです。しんどさは他人と比べるものではありません。
次回からは、具体的な困りごとに対してどうアプローチしていくか、見ていきましょう。
一緒に、ラクになる方法を探しに行きましょう!
【発達障害・学習障害のお子様がいるご家庭の保護者相談】
発達障害・学習障害のご家庭への、保護者相談を行っています。
通常の育児と同じく、発達障害・学習障害をお持ちのお子様との生活は、キラキラしたものばかりではありません。
「傷ついた人は間に合わせの包帯が必ずしも清潔であることを要求しない」
三島由紀夫の言葉ですが、この言葉の通り、多くの本に書かれている「理想の理論」は時に全く役に立ちません。
現実の生活に基づいた、現実的なそれでいて明るい未来が見える支援を常に心に置いています。
是非お困りごとをお聞かせください。
※初回はクーポンにて大幅割引ができますので、是非ご利用ください。詳細はバナーから。







コメント