・算数でお困りの人
・算数障害を知りたい人
・「おおよその数が分からない」の支援・対処法が知りたい人

頭で生きようとする人にとって、気持ちは時に「正しくない」。
でも、気持ちを「正しい」とすれば、全て正しい。
自尊心は守られ健康も守られる。
コントロールできないものを中心に生きよう。
どうも、ひつじぃです。
はじめに
今回は、「おおよその数が分からない」に対する支援・対処法を見ていきます。
数概念ってなに?という人はこちらへどうぞ。
ごーごごー。

今回は基数性だよ!
対象の困りごと
① 数を数えることはできるが、おおよその数が分からない。
例:部屋の端から端まで「だいたい何歩か」が分からない
② 計算式が書いてあれば計算ができるが、数のまとまりを見つけたり分けたりといったことが難しい。
例:文章題や図形問題の立式ができない
③ 数直線が苦手。
例:10と50の間に4本線があると、その4本目は「14」と数えてしまう
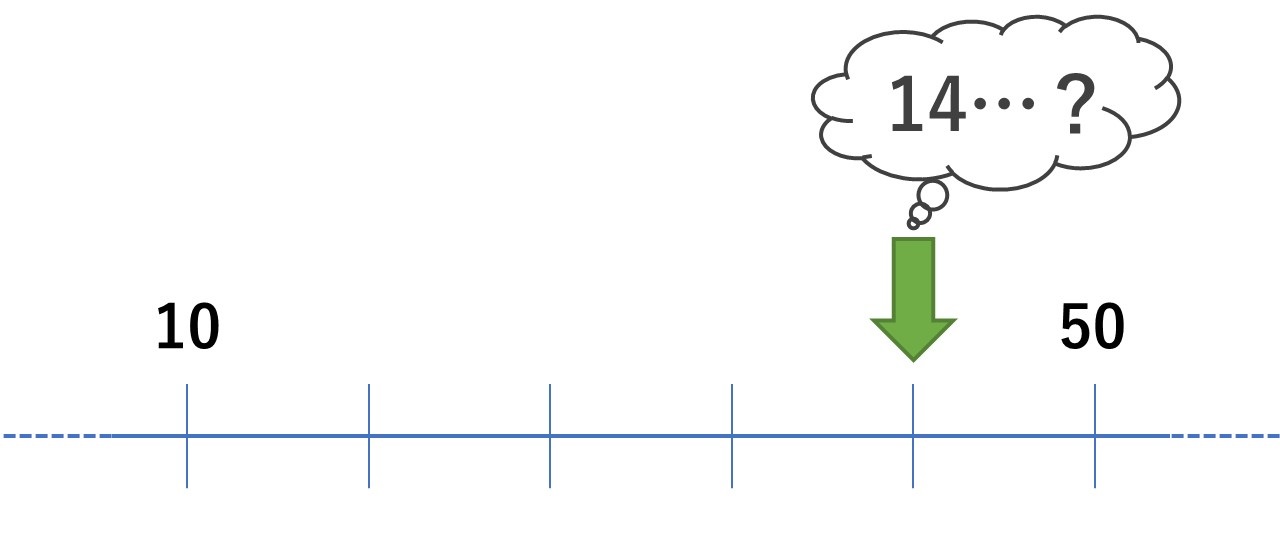
④ 数の大きさを線の長さで表すのが苦手。
例:「1」を表した線と「5」を表した線の長さが一緒になってしまう
事前に考えるべき点(前記事と同じ)
前記事と同じ内容ですが、欠かすことができないもののため、記載します。
すでにご覧になった方は、次に進んでください。
視覚に異常はないか。
眼球運動に異常があると、数字が認識できません。よって、違う数字でも判別が難しくなります。
また、桁の認識も難しくなると考えられます。
ADHDの不注意特性はないか。
モノを数える際、注意が大きくそれてしまい一瞬数を数えることから意識がそれている可能性があります。
そうすると、正しく数えることは難しいと思われます。
聴覚に異常はないか。
聴覚に異常があると、数詞の音が聞き取れません。そのために発音を間違えていたり、判別ができていない可能性があります。
ワーキングメモリーに異常はないか。
視覚的・聴覚的ワーキングメモリーに異常があると、数を数える際に覚えていられません。
視覚や聴覚は医療機関に、不注意・ワーキングメモリーはWISC等の検査で分かります。
これらがクリアできていたら、次の項目へ進みましょう。
支援・対処法
基数性・序数性について
復習です。詳しくはこちらの記事へどうぞ。
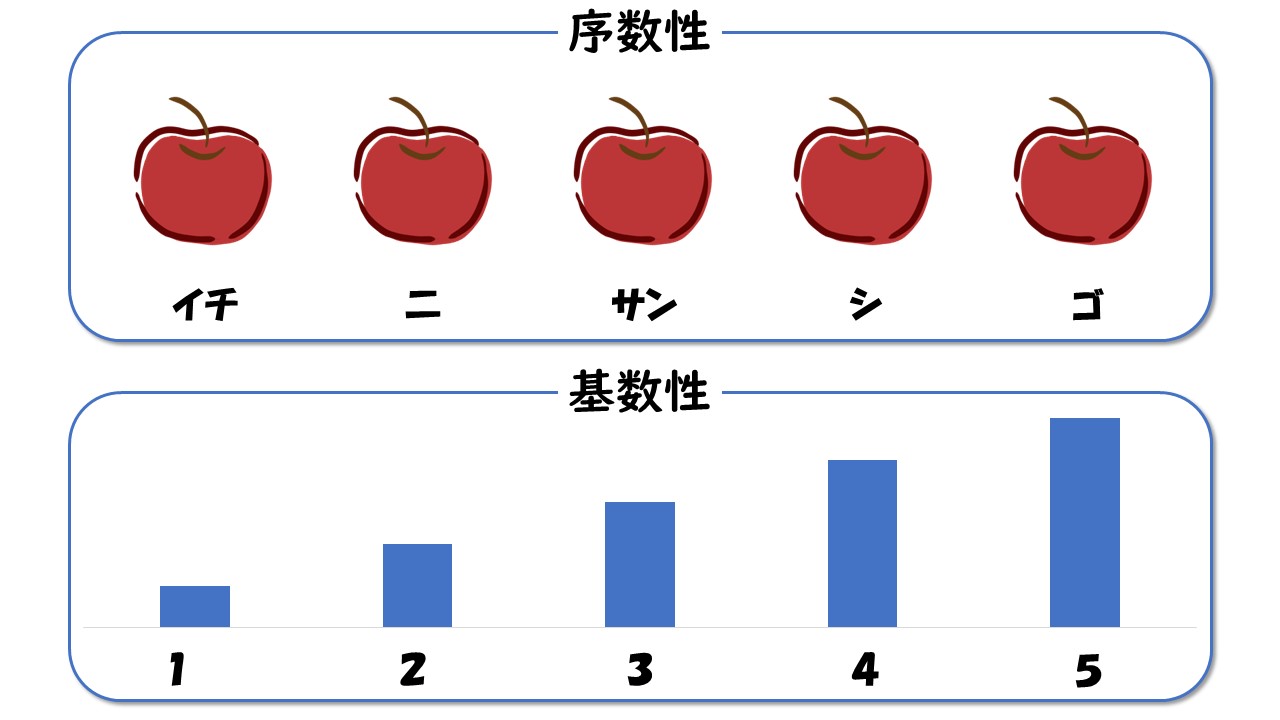
序数性は「数を数えること」、基数性は「数の大きさを把握すること」と関連します。
これにより、今回の困りごとは「序数性は理解できているが、基数性は理解できていない」状況だと分かります。
メカニズム
序数性・基数性の理解には、認知処理特性が大きく関わってきます。
序数性は「数を数えること」=「数が順序を表していることの理解」です。
系列的に順序で考えるのは、継次処理能力が大きく関わります。
基数性は「数の大きさを把握すること」=「数が量を表していることの理解」です。
概念的に考えるのは、同時処理能力が大きく関わります。
今回は基数性なので、こちらに焦点を当てて考えてみます。
小学校3年生くらいまでの計算であれば、基数性は理解できなくても解くことができます。
しかし「おおよその数が分からない」ということは「数のまとまり(集合)」が分からないということです。
つまり、「数えることはできるが、『◯個集める』ということが困難」ということです。
これが日常生活だと「100円で何が買え、1000円で何が買えるか」の検討をつけるのが難しくなります。
また、貯金額や財布の中を見て「どれくらいの量のお金か」というのが分かりません。
また、「数が量を表している」という考え方は、文章題に深く関わり、立式が難しくなります。
こういった苦手は、お金を扱い始める・文章題が本格化しだす小学3年生あたりから困りごととして表れやすくなります。
序数性の習得の工夫
サイコロ遊び
サイコロ遊びをやってみましょう!
【遊び方】
① サイコロを投げます。
② 出た目を「すうじ」の四角の中に書きます。
③ 出た目の数だけ、「スタート」の下の丸を左から順になぞります。
④ なぞった丸の分だけ、「スタート」の下の点線の上から実線を左から引きます。
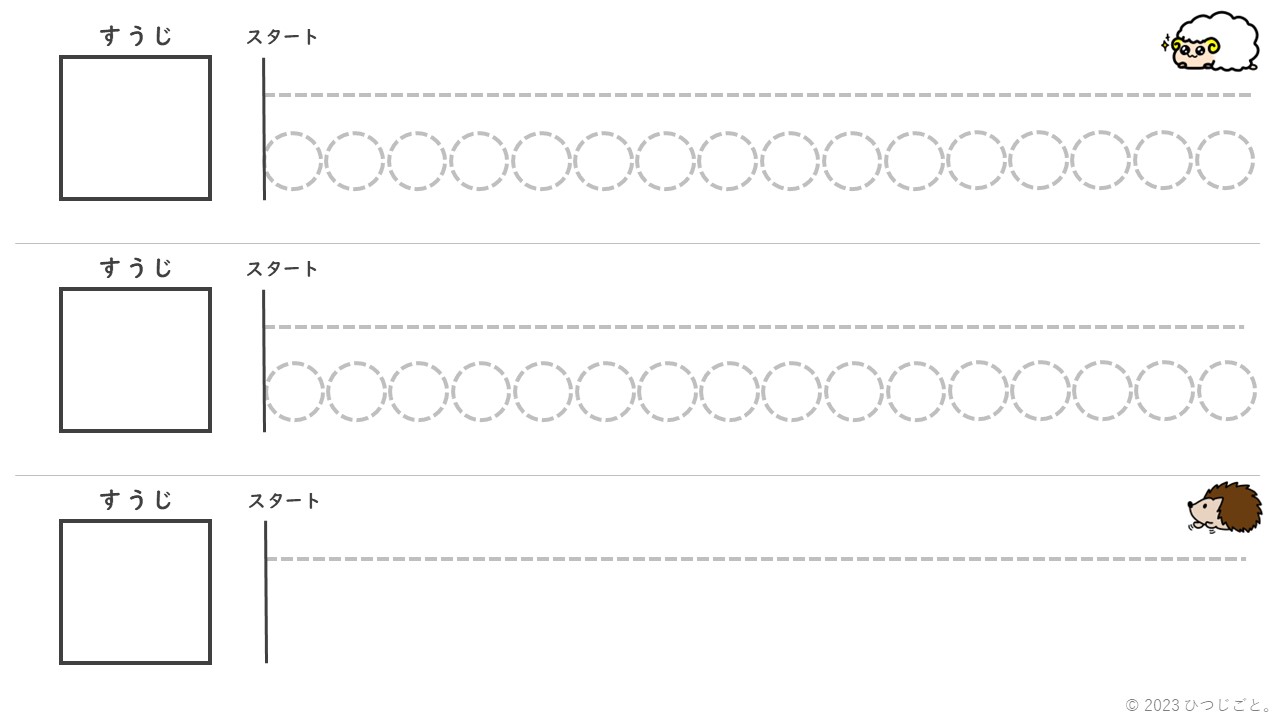
※ご自由にコピーしてお使いください。後日といろプリントにて、ハリーが手直ししたものが公開されます。
このすごろくの目的は、
・数字に対して、数量を分離量と連続量で表し、「数の量感」を習得する
・数字を分離量で表すことで、「まとまり」と数を紐付ける
です。
数概念の基数性の理解の困難は、連続量(数えられない量)の把握の難しさに繋がります。
序数性に困難がなければ「1つずつ数える」ことはできると思いますので、「1つずつ数えてなぞった丸(分離量)の長さ」を直線という「連続量」で表し、
分離量と連続量の感覚の一致、また逆に分離量をまとまりとして捉える、ということの習得を目指します。
慣れてきたら、③と④を逆にして、直線(連続量)から描いて丸(分離量)の長さと比較してみる、ということをやってみても良いかもしれません。その場合は3つ目の回答枠を使ってください。
この際、帳尻を合わせるように丸を大きく(小さく)描いても良しとします。
「できた!」という喜びを原動力に習得へ向かうものですし、その場合は分離量と連続量が一致していれば半分は習得に向かえているわけですので、「できた!」という喜びを認める方向でOKです。
また、お気に入りのシールを使っても良いですね。点線の丸は直径1.5cmにしてあります。
注意点(前記事と同じ)
前記事と同じ内容ですが、欠かすことができないもののため、記載します。
すでにご覧になった方は、次に進んでください。
考える順番
① これは算数障害の問題なのか
② 算数障害であれば四領域のどこに困難があるのか
③ 領域の中の具体的にどういった点に苦手があるのか
必ずこの順で考えるようにしてください。
この記事をはじめから辿っていけば大丈夫です。
間違えることへの恐怖
「苦手な子はどれだけ強がっていても『できなかったらどうしよう』と常に思っている」
これを忘れないことを徹底して欲しいと切に願います。
正確には、恐れているのは「間違えること」ではありません。
間違えることによって「どう思われるか」です。
しかしこれは本人の中のことであり、「だったら周りがどう思っているか伝えればいいよね」は100%の回答に絶対なりません。
どれだけ「大丈夫」と言っても、「もしかしたら」が拭いきれない、そのくらいの気持ちの中に彼らはいると考えてもらえたらと思います。
試してもできない時
「試してもどうしてもできない」ということも、もちろんあります(脳機能障害からくるLDなど)。
その場合は、
「これ以上続けて本人の自尊心が低下すること」
「能力を獲得しラクに生きることができること」
この2つを天秤にかけ、必ず本人の気持ちを聞いてください。
勉強は「ラクに生きる可能性を広げるためにするもの」です。
その勉強によって結果的に自尊心が低下し、可能性が狭まってしまうようなことは絶対に避けるべきです。
どうしてもできない場合は、トップダウンでツールに頼ればいいのです。
スマホをかざせば「何個あるか」を表示してくれるものもあります。
「習得は絶対ではないこと」
「どこまで学習すべきかの判断基準を常に持つこと」
この2つを必ず心に留めて、「本人と一緒に」取り組んでいただきたく思います。


おわりに
さて、今回は数概念の基数性に関して見ていきました。
日常の困りごととしてはお金、算数的には文章題とよく見られる困りごとながら、「え、そこが難しかったの?」という驚きもあるかもしれません。
数が量を表しているということは、自然に習得できる人にとっては改めて考えることすらないことであり、それゆえに算数障害は今でも理解がされにくい環境にあります。
理解が及ばないところを補うのは、いつの世でも「知識」ですね。
さて次回は、計算の習得についてご紹介します。
それではまたお逢いしましょう。
みかんは連続量なので、どれだけ食べても大丈夫(謎)!
【発達障害・学習障害のお子様がいるご家庭の保護者相談】
発達障害・学習障害のご家庭への、保護者相談を行っています。
通常の育児と同じく、発達障害・学習障害をお持ちのお子様との生活は、キラキラしたものばかりではありません。
「傷ついた人は間に合わせの包帯が必ずしも清潔であることを要求しない」
三島由紀夫の言葉ですが、この言葉の通り、多くの本に書かれている「理想の理論」は時に全く役に立ちません。
現実の生活に基づいた、現実的なそれでいて明るい未来が見える支援を常に心に置いています。
是非お困りごとをお聞かせください。
※初回はクーポンにて大幅割引ができますので、是非ご利用ください。詳細はバナーから。









コメント